Draft overviews for VCE Mathematics (General, Methods, and Specialist 2023 study design)
You thought I was going to stop at comparing curricula?
Because I couldn’t stop my brain after sequencing all of Years 7–10 with Ochre Education, it started trying to sort out VCE on its own. I was just along for the ride. Here is the culmination of that sequencing (and cross-checking against other curricula) work.
What should I expect?
overviews that sequence the content from the 2023 VCE Mathematics study design, including making a concurrent Methods and Specialist courses without pre-teaching Methods content inside of Specialist possible.
to be usable right now, even just to incorporate ideas into your current scheme of work or scope and sequence.
a beg, borrow, and steal of the best ideas from across Australian curricula and beyond, with considerations taken from a number of high-performing international curricula.
more details about what the current study design actually entails.
numbered topics, subtopics, and content points for easy reference.
content points beginning with command verbs (as much as possible).
non-study design content flagged in red that could be included for extension (or possible changes to future study designs to consider).
suggested assessments timings and flagging of non-SAC assessments for units 3&4.
the same attention to detail you would expect from me.
iterative improvements as noted by the version number in the file name (major changes, minor changes, error corrections), which I will aim to keep a changelog of in the document.
What shouldn’t I expect?
an idealised study design. It is intended that it could be used by teachers now if they want to. It is not intended to be a submission to the VCAA for the next study design.
classroom tested rigour. These are theoretically planned, intended to get the most of these subjects as possible. They will need feedback and iteration to ensure they are watertight and sensible for actual classroom teaching and learning.
no errors. While these have been discussed in varying amounts with a few people which has picked up on some errors already, this is predominantly a one-man job and has gone through a lot of changing and editing. So, it is more than likely that things have slipped through as these documents developed over the past several months. Do reach out if you spot anything.
all of the suggested structural changes suggested in the comparison blogposts. Since this is designed to be usable now, I’ve intentionally not made some changes.
perfect subtopic breakdown. Some subtopics were created solely because I couldn’t keep one larger one to a page and refused to have any be longer than a page for usability reasons.
What’s the plan from here?
As I go back to my normal working schedule, I’m planning on blogging my way through these (and other things), discussing decisions of sequencing, inclusions, exclusions, and the suggested non-study design content as well as looking for ways to improve them (of which General already has a target on its back, just from things learnt while progressing through writing them that Methods already got in full but General got to a smaller extent).
I welcome initial feedback (prior to me going through them in detail) on ways they can be further improved and any errors or oversights made. I’d love to hear from
local Australian teachers who are familiar with these courses,
international teachers who teach courses with similar content,
secondary teachers who teach these courses day-in and day-out, and
university-level teachers who teach what comes after to ensure that these form a solid foundation.
If you have thoughts or questions or just want to chat about them, reach out on Substack, on socials (Twitter/X, Bluesky, LinkedIn), or via email.
I want this to become a basis that can be adapted not just locally in Victoria, but also throughout Australia and beyond. The more eyes on it that can make it the best it can be, the better. So, sharing this around is appreciated.
Without further ado, here they are.
General Mathematics overview

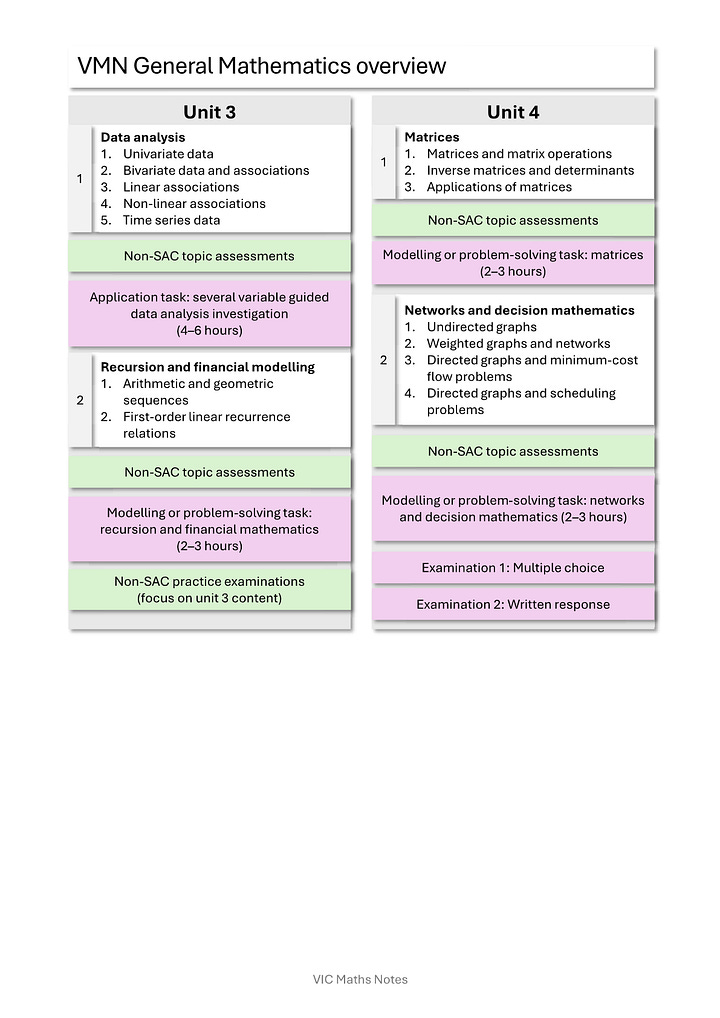
Highlights
an initial preliminary topic to ensure foundational proportional reasoning and rounding knowledge and skills are in place.
the measurement content as early in unit 2 as possible (though you could adapt to put in unit 1 if you are less fussy about following the content unit-by-unit.
unit 1&2 content sequenced so that topics can build on each other.
unit 3&4 content points rightfully described as review when coming from units 1&2 so teachers can make better decisions about how long to linger on them.
Click here to see the General Mathematics overview.
Mathematical Methods overview
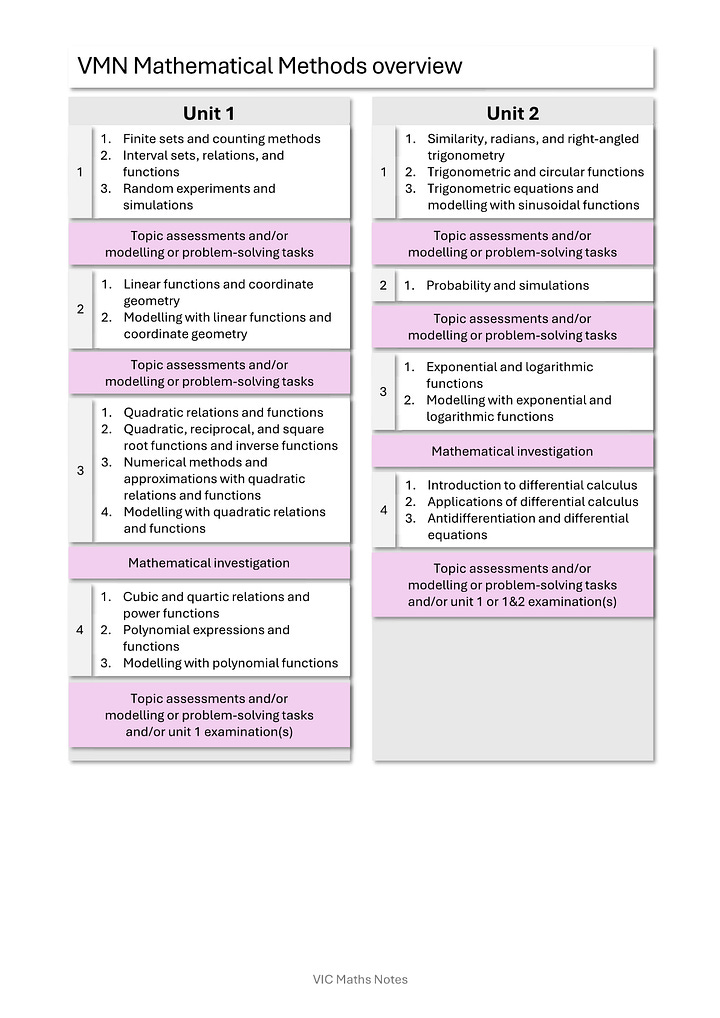

Highlights
units 1&2 designed to embed calculus concepts of ratios and rates of change, and accumulation and area starting from linear functions and ever present throughout to create a strong identity for the subject, and to help keep review content from previous years feeling fresh.
units 3&4 embed calculus from the start rather than ignoring it and covers all core calculus ideas with polynomial functions before moving on and then continues to make the calculus with additional functions the motivator for reviewing them.
units 1&2 designed to build relations and functions from the ground up from sets.
unit 2&3 anti-differentiation introduced as solving differential equations to keep the surprise relationship between differentiation and integration for later in unit 3.
unit 3 designed to focus on calculus and modelling with base functions (though chain, product, and quotient rules are introduced) and unit 4 designed to focus on the combinations of functions and their use in modelling.
final unit 4 topic designed to prepare students for exam 2 style modelling problems, such as generalising features of functions with a parameter.
relevant pseudocode mentions throughout rather than ad hoc at the end.
sequenced so that Specialist Mathematics should reasonably always follow on from Mathematical Methods all the way through to sampling.
Click here to see the Mathematical Methods overview.
Breakdown posts
Specialist Mathematics overview
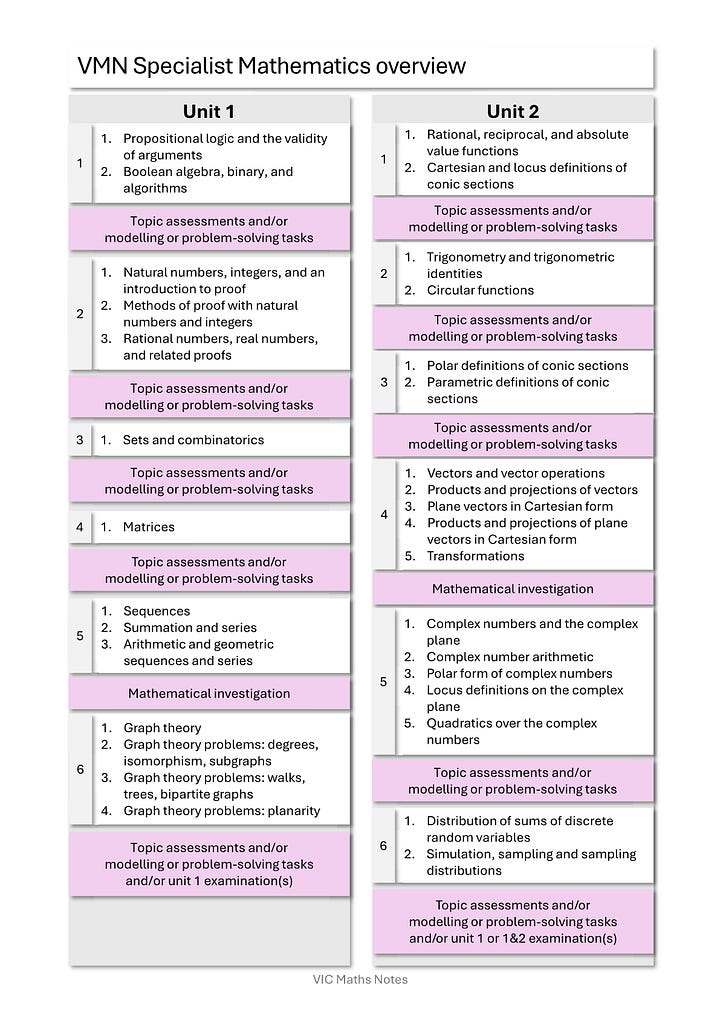
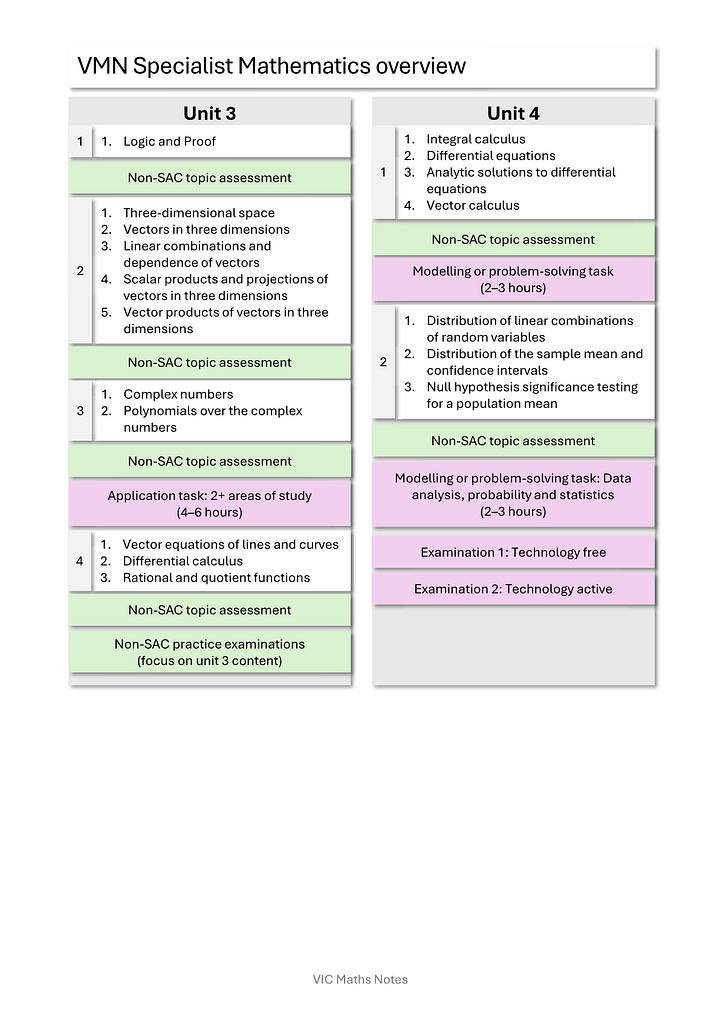
Highlights
units 1&2 begin with formal logic and proof to ensure students have a solid proof foundation for the whole subject.
units 1&2 repeatedly focus topics around the field axioms in various contexts.
units 1&2 vectors are built up from directions and magnitudes first prior to Cartesian form being introduced.
unit 3 lines and planes in three dimensions in Cartesian form taught prior to vector equations for a basis to work from.
unit 3 vector products built up from first principles.
relevant pseudocode mentions throughout rather than ad hoc at the end.
sequenced so that Specialist Mathematics should reasonably always follow on from Mathematical Methods all the way through to sampling.
Click here to see the Specialist Mathematics overview.


Do one for QLD next!!
For real though, as someone who has taught VCE maths and has been in maths leadership in Victorian secondary schools, these are phenomenal. What a brilliant resource to share.
Putting my Methods teacher hat on for a moment, the sequencing here is incredible. You've nailed it. Rather than slamming calculus together and wondering why the topic isn't done as well as we'd like - especially when apps of calculus forms such a large part of the exam - distributing it allows for constant review and reinforcement. Calculus feeds into so many of the other topics in the SD, and so treating it as a standalone has never made sense. Terrific sequencing from one of the best.